If you had told me a couple of years ago that I’d be voluntarily spending my free time deriving moment generating functions or getting hyped about the Generalized Stokes Theorem, I would have assumed you were talking about someone else.

I didn't grow up identifying as a "math person," but I also didn't think I was incapable of it. Deep down, I knew I could learn it if I really tried. The problem was that I wasn't good at it because I never knew what it was for. My brain simply refused to retain abstract rules without a purpose. If only someone had told me back then that these equations were the keys to building the future—that they were the language of physics, machines, robots, intelligence, and all the cool stuff—things might have been different.

Fast forward to my career as a full-stack engineer. I was doing fine, but I had this nagging goal: I wanted to really understand AI and robotics. My motivation was never to merely implement libraries or stitch together APIs. I wanted to know how to make things move. I wanted to know how LLMs and neural networks actually worked under the hood. I wanted to know how the heck we made rocks and sand think.

Every time I opened a deep learning textbook or tried to read something like the Modern Robotics text to find those answers, I hit a wall of arcane runes. I realized I couldn't wing the math anymore. I needed a baseline.

Enter Math Academy.

This post is a look back at my journey through the platform over the last year or so. It’s been a wild ride from struggling with basic sketching to being in the "endgame," hunting for hidden "easter egg" lessons from unreleased courses.

The Grind and the "Sustenance"

Let's be real, the journey is a grind. It has to be.

I started with the Foundations. Early on, it was a rush. I was soaking up new material constantly. But the real test of discipline came later. I remember days deep into the curriculum where the ratio of reviews to new lessons started to feel painful. I’d have to churn through tons of reviews and quizzes to earn a sliver of new material because I had so much knowledge to maintain.

I even went through a phase of ditching my iPad and going back to pen and paper (specifically a nice Kuru Toga mechanical pencil) because I needed to feel the math—a visceral aspect to an intellectual pursuit. There’s something satisfying about building a physical stack of notebooks filled with solved problems. That was my daily "math sustenance."

The Scoreboard

Eventually, the grind paid off. After racking up close to 30,000 XP, I managed to clear the board.

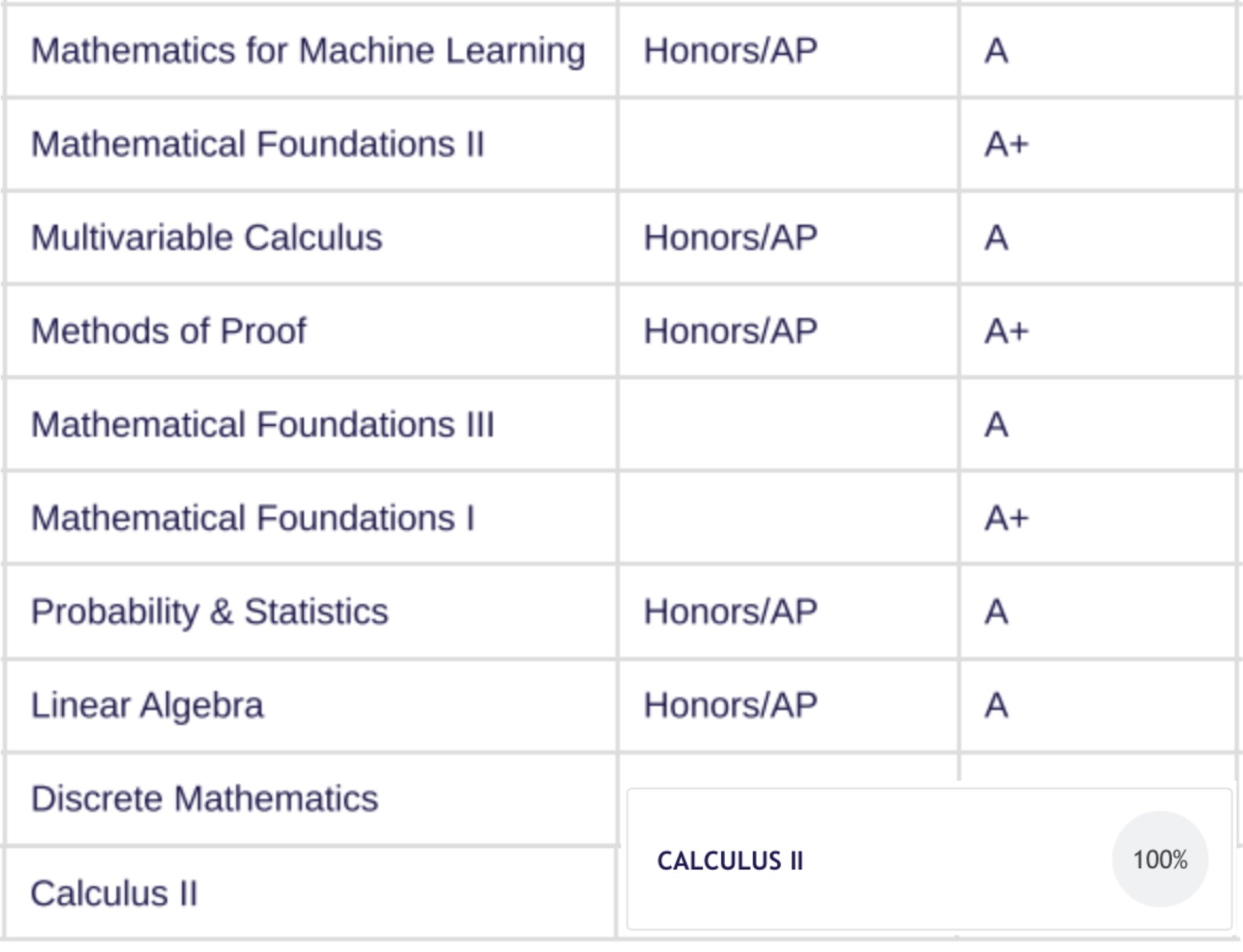
If I had to pick a favorite, it was Mathematics for Machine Learning (M4ML). Completing it felt like the biggest achievement because it forced me to learn a massive amount of Multivariable Calculus, Probability, and Linear Algebra very quickly. It was the course that finally made me feel "ready."

That said, the standalone Multivariable Calculus course deserves a shoutout. It notably had a lot of excellent diagrams that made visualizing the geometry much easier. And honestly? It just felt really cool doing triple integrals and handling the advanced multivariable stuff. There is a specific aesthetic satisfaction to solving those problems that makes you feel powerful.

The Linear Algebra Gauntlet

However, I have to make a special mention for Linear Algebra.

Looking back, this was arguably the most impactful course of the entire curriculum. It is elegant and profound—the absolute bedrock of everything in AI, graphics, and robotics. Without it, the robotics textbook I'm reading now would be impossible.

But man, did I hate the process at the time. It was a total roller coaster.

I hated the manual matmuls. I hated calculating determinants by hand. I hated subspace projections. It felt tedious, mechanical, and endless. I wanted to scream, "I have a GPU for this!" Let’s just say I frequently stress-tested the structural integrity of my desk.

But I grinded through them. I forced myself to do the reps because I knew I couldn't just "import numpy" my way through understanding the underlying geometry. And in hindsight, that manual suffering is exactly why the concepts stick now.

The "Aha!" Moments

The grind started paying off in these incredible moments where things just clicked. I remember when I finally groked what Stoke's Theorem represented; I literally felt complete.

Or the day I woke up and realized I hadn't proved Euler's formula yet, and sat down and did it because I finally had the tools from the infinite series lessons.

Then came Methods of Proof. Learning induction and realizing the inductive step is where you attempt to assert dominance over the math? Incredible.

The Endgame

With the main stack defeated, I entered a sort of "endgame" state. I started getting served "easter egg" lessons from the unreleased courses.

When I got to Abstract Algebra, I started treating the math itself like software. I realized I could define mathematical structures the same way I define APIs. I started building these "Math APIs" in Anki—defining a Ring not as a fuzzy concept, but strictly as an Abelian Group under addition and a Monoid under multiplication.

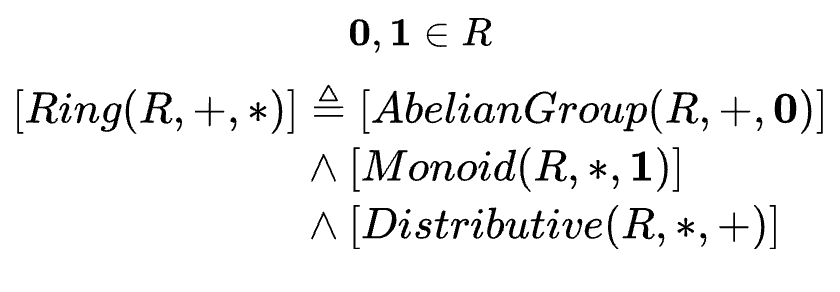
It turned abstract theory into clean, logical architecture.

And finally, Differential Equations. Nothing beats it. I would say I had the most fun here. It’s like being a dual-wielding samurai, gracefully using one blade of differentiation and the other of integration. Whether I was tackling Cauchy-Euler equations or using Laplace transforms to teleport between domains, it felt like pure wizardry.

Whenever I do these problems, I always remember this specific news story where an economist was kicked off a flight because a passenger thought his math was "terrorist code."

It sounds wild, but I get it. To the uninitiated, these symbols look like dangerous, arcane power. And I get to write them.

The Unlock: Access to the Bleeding Edge

The real victory, however, was what I was doing while I was tackling those unreleased lessons.

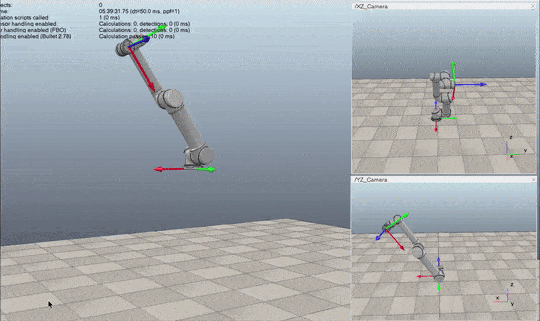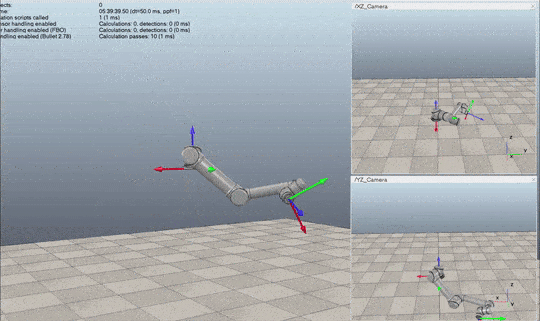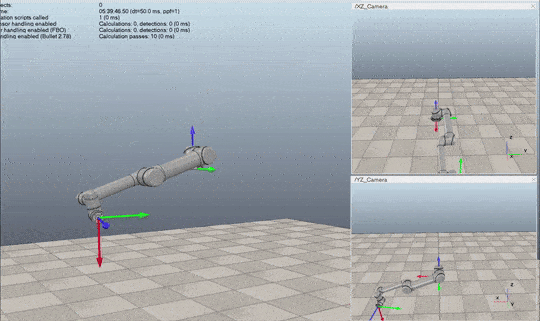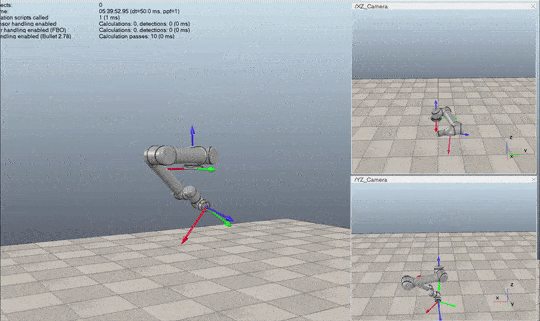
I started working through the Modern Robotics textbook—a book that is notoriously math-heavy. A year ago, a page like this would have crushed me. It looks like alien hieroglyphics.

The ultimate boss fight was Chapter 8: Dynamics of Open Chains. It is easily the hardest part of the book. The authors skip a lot of steps, assuming you can bridge the gap yourself. Before Math Academy, these gaps would have been game-over for me. But because of the Linear Algebra and Multivariable Calculus I had grinded through, I could actually fill in the omitted steps myself. It was hard, but it was doable.

Justin Skycak (from Math Academy) actually quoted me on this specific struggle. He put it perfectly: filling your foundations turns these "omitted steps" from uncrossable chasms into minor potholes.

Because I didn't have to fight the notation, I could focus on the concepts.

I got familiar with Lie algebras, which are fundamental to the text. I finally understood the relationship between the Lie groups $SO(3)$ and $SE(3)$ and their algebra counterparts $so(3)$ and $se(3)$. I learned how to handle the transformations between them, mapping twists and exponential coordinates into the actual rigid body motions that drive the robot.

That math directly translated into code. I managed to implement Forward and Inverse Kinematics from scratch.

I used Lagrangians to derive the equations of motion for gravity and physics simulation, then advanced to the 6D Newton-Euler formulation. By leveraging Lie algebra adjoint operators, I was able to define the recursive dynamics as clean, structured equations rather than a mess of scalar components.

I wasn't just reading it. I was able to take those equations and actually build things.

It wasn't just robotics, either. This new literacy unlocked the core research papers I had always wanted to understand. I remember opening the original Batch Normalization paper—a foundational text in deep learning—and realizing I could actually read it. Not just the abstract and conclusion, but the math in the middle. I sat down and derived the backpropagation equations for the batch norm layer myself, from scratch.

That feeling—going from being intimidated by the symbols to wielding them as tools—is hard to describe. It’s a permanent shift in perspective, and it’s one I owe entirely to the work I put in over the last year.

Developing the Love for Math

Math is strange. Concepts like linearity often seem trivial at first—why care that $f(a+b)=f(a)+f(b)$? My brain used to dump these "boring" rules because it couldn't grasp the implications.

But as I pushed further, I began to discover elegant structures that showed profoundly different facets of the same concept. I realized that vector spaces, inner products, eigenvalues, and transformations all hang off that one simple rule. Linearity wasn't an isolated node anymore; it was a main branch of the tree.

Suddenly, the mist clears. You realize you aren't just memorizing rules; you are uncovering a beautiful, interconnected landscape.

I am grateful to be alive in the era where Math Academy and LLMs exist. Math Academy is the intense gym for deliberate practice and automaticity, and LLMs serve as my personal Richard Feynman. It's easier to spot connections and have a bird's eye view of the surrounding math landscape. Learning math no longer feels like stumbling through a dense fog. It feels like a pleasurable walk through a misty morning, watching the magnificent peaks and valleys slowly come into view.

A Massive Thank You

Right now, I’ve paused the daily math grind to focus on building Haeru, a startup I cofounded. But the goal is to come back. I plan to return to the math, AI, and robotics grind in the near future—hopefully with the freedom to make exploring the bleeding edge the only thing I do.

I have to end this by giving unbelievable amounts of credit to the team at Math Academy, specifically folks like Justin (@justinskycak) and Alex (@ninja_maths).

I cannot believe I learned all of this math in less than a year. It genuinely changed my life. They are taking subjects that gatekeep entire industries—physics, engineering, AI, and robotics—and making them accessible through sheer, scientifically-backed rigor.

It’s hard work, but it’s the most rewarding work I’ve done. If you are sitting on the fence thinking you aren't a "math person," trust the process. You might unlock some latent powers you didn't know you had.

On to more math.